এবারে এসেছি আমরা সবচেয়ে মজার অংশটুকুতে। সমতল আয়না এবং উত্তল আয়নায় শুধু একধরনের প্রতিবিম্ব তৈরি হতো। অবতল আয়নায় দুই ধরনের প্রতিবিম্ব হতে পারে। একটা বস্তু ফোকাস দূরত্ব থেকে কম দূরত্বে রাখলে একধরনের প্রতিবিম্ব তৈরি হয়, ফোকাস দূরত্ব থেকে বেশি দূরত্বে রাখলে অন্য রকম প্রতিবিম্ব তৈরি হয়।
সেটি শুরু করার আগে আমরা আলোক রশ্মি গোলীয় অবতল আয়নায় কীভাবে প্রতিফলিত হয় সেটি জেনে নেই। গোলীয় অবতল আয়নায় তিনটি বিশেষ আলোক রশ্মির প্রতিফলনের নিয়ম জানলেই কীভাবে প্রতিবিম্ব তৈরি হয় সেটি ব্যাখ্যা করতে পারব:
(i) আলোক রশ্মি ব্যাসার্ধ বরাবর বা কেন্দ্র থেকে শুরু হলে সেটি লম্বভাবে প্রতিফলিত হয়ে যেদিক থেকে এসেছে ঠিক সেদিকেই ফিরে যায়।
(ii) প্রধান অক্ষের সমান্তরাল রশ্মিটি প্রতিফলনের পর ফোকাস বিন্দু দিয়ে যাবে।
(iii) আলোক রশ্মির দিক পরিবর্তন করা হলে এটি যেদিক থেকে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। কাজেই কোনো আলোক রশ্মি ফোকাস দিয়ে গেলে সেটি প্রধান অক্ষের সাথে সমান্তরাল হয়ে প্রতিফলিত হবে।
এবারে আমরা অবতল আয়নার জন্য প্রতিবিম্ব তৈরি করতে পারব।
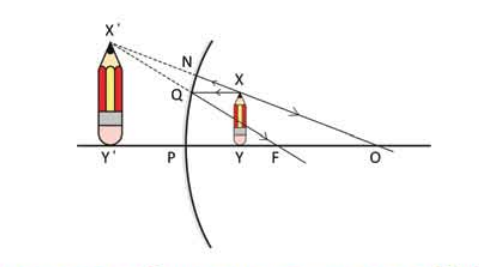
চিত্র 8. 22:অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের ভেতরে রাখা হলে প্রতিবিম্ব বড় দেখায়
8.07 চিত্রে একটি অবতল আয়না দেখানো হয়েছে। অবতল আয়নাটি যে গোলকের অংশ সেই গোলকের কেন্দ্র হচ্ছে O, অবতল আয়নার ফোকাস বিন্দু F এবং ধরা যাক XY বস্তুটির প্রতিবিম্বটি আমরা বের করতে চাই। Y বিন্দুটি থেকে আলো অবতল আয়নার P বিন্দুতে প্রতিফলিত হয়ে আবার Y হয়ে O বিন্দুর দিকে ফিরে যাবে। কাজেই বোঝা যাচ্ছে এটি OP রেখায় কিংবা তার বর্ধিত অংশের কোনো একটা বিন্দুতে থাকবে, ঠিক কোথায় সেই বিন্দুটি হবে সেটি বের করতে হলে Y বিন্দু থেকে অন্যদিকে আরো একটি রশ্মিকে অবতল আয়নার দিকে আঁকতে হবে, আমরা আর সেটি করছি না, আগের মতো X বিন্দুটির প্রতিবিম্ব বের করতে পারলেই সেখান থেকে Y বিন্দুটির প্রতিবিম্বের সঠিক জায়গাটি বের করা যাবে। X বিন্দুর প্রতিবিম্ব বের করতে হলে এই বিন্দু থেকে দুটি রেখা আঁকতে হবে, বোঝাই যাচ্ছে প্রথম রেখাটি হবে OX রেখার বর্ধিত অংশ, এটা অবতল আয়নাকে লম্বভাবে স্পর্শ করে ঠিক সেই পথেই প্রতিফলিত হয়ে ফিরে যাবে। চিত্রে যেভাবে দেখানো হয়েছে X বিন্দু থেকে আরেকটা রশ্মি হতে পারে অক্ষের সাথে সমান্তরাল একটা রশ্মি, কারণ আমরা এর মধ্যে জেনে গেছি সমান্তরাল রশ্মি প্রতিফলনের পর ফোকাস বিন্দু দিয়ে যায়। কাজেই এটা Q বিন্দুতে আপতিত হয়ে প্রতিফলিত হয়ে F বিন্দু দিয়ে চলে যাবে।
X বিন্দু থেকে বের হওয়া দুটি রশ্মি প্রতিফলনের পর NO এবং OF এর দিকে যাবে এবং দেখাই যাচ্ছে এই রশ্মি দুটো মিলিত হবার কোনো সুযোগ নেই। কাজেই ডান পাশে কোনো প্রতিবিম্ব তৈরি হতে পারবে না। কিন্তু যদি ডান পাশ থেকে বাম পাশে তাকানো যায় তাহলে মনে হবে ON রেখা এবং FQ রেখা দুটি বুঝি x' বিন্দুতে মিলিত হয়েছে— কাজেই x হবে X এর প্রতিবিম্ব। এই বিন্দু থেকে OP অক্ষের ওপর একটি লম্ব আঁকলেই আমরা XY এর পুরো প্রতিবিম্ব XY' পেয়ে যাব। x y থেকে সত্যিকারভাবে কোনো আলো যাচ্ছে না, শুধু আমাদের মনে হচ্ছে এখানে বুঝি প্রতিবিম্বটি তৈরি হয়েছে। কাজেই এই প্রতিবিম্বটি অবাস্তব প্রতিবিম্ব। চিত্র থেকে দেখা যাচ্ছে প্রতিবিম্বটি মূল বস্তু থেকে বড়। শুধু তা-ই নয় আমরা বস্তুটিকে যতই ফোকাস বিন্দুর কাছে আনব, প্রতিবিম্বটি ততই বড় হবে। (যদি এটাকে ঠিক ফোকাস বিন্দুতে বসানো হয় তাহলে প্রতিফলিত আলোক রশ্মি আসলে সমান্তরাল হয়ে যাবে অর্থাৎ প্রতিবিম্ব তৈরি করার জন্য আলোক রশ্মি আর মিলিত হতে পারবে না।
এবারে অবতল আয়নায় ফোকাস দূরত্বের ভেতরে কোনো কিছু রাখা হলে তার প্রতিবিম্বটি কেমন হবে সেটি দেখে নেওয়া যাক :
(a) প্রতিবিম্বটির অবস্থান কোথায় হবে সেটি নির্ভর করবে আসল বস্তুটির অবস্থানের ওপর। বস্তুটি যতই ফোকাসের কাছে রাখা হবে প্রতিবিম্বের অবস্থানটি হবে তত দূরে।
(b) এটি অবাস্তব
(c) সোজা
(d) প্রতিবিম্বটির দৈর্ঘ্যও নির্ভর করবে তার অবস্থানের ওপর, যত ফোকাস বিন্দুর কাছে যাবে তার দৈর্ঘ্যও তত বেড়ে যাবে।
আমরা এখন পর্যন্ত যত প্রতিবিম্ব দেখেছি তার মাঝে এই প্রতিবিম্বটি সবচেয়ে চমকপ্রদ, কারণ এই প্রথমবার আমরা একটি বাস্তব প্রতিবিম্ব দেখব, অর্থাৎ যেখানে প্রতিবিম্বটি তৈরি হবে, সেখানে সত্যি সত্যি আলো কেন্দ্ৰীভূত হবে(চিত্র 8.08)।
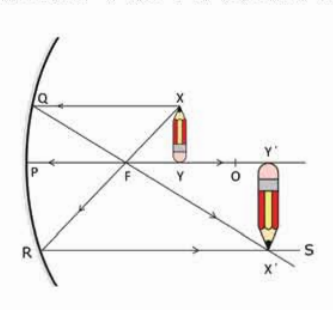
চিত্র 8.23: অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের বাইরে রাখলে প্রতিবিম্বটি হয় উল্টো।
সত্যিকারের বস্তুটি হচ্ছে XY এবং Y বিন্দুর প্রতিবিম্বটি অন্যবারের মতো নিশ্চয়ই YP রেখার উপরে থাকবে। x বিন্দুটির প্রতিবিম্ব বের করার জন্য আমাদের দুটি রশ্মি আঁকতে হবে। একটি হবে অক্ষের সাথে সমান্তরাল XQ এবং প্রতিফলিত হয়ে এটি নিশ্চয়ই ফোকাস বিন্দু F এর ভেতর দিয়ে QF হিসেবে যাবে। দ্বিতীয় রশ্মিটি আমরা F বিন্দুর ভেতর দিয়ে আঁকতে পারি। এটি অবতল আয়নার প্রতিফলিত হয়ে RS হিসেবে সমান্তরাল হয়ে যাবে, কারণ সমান্তরাল রেখার আলো অবতল আয়নাতে প্রতিফলিত হয়ে যে রকম ফোকাস বিন্দুর ভেতর দিয়ে যার ঠিক সে রকম তার উল্টোটাও সত্যি, আলো সব সময়ই তার গতিপথ উল্টো পথে পুরোপুরি অনুসরণ করে। QF এবং RS রেখা দুটি X' বিন্দুতে ছেদ করেছে এবং X' বিন্দুটি হচ্ছে X বিন্দুর প্রতিবিম্ব। কাজেই X' বিন্দু থেকে PO রেখার ওপর লম্বটি Y' বিন্দুতে ছেদ করেছে এবং X'Y' হচ্ছে XY এর প্রতিবিম্ব। দেখতেই পাচ্ছ এই প্রতিবিম্বটি এখন পর্যন্ত দেখা অন্যান্য প্রতিবিম্ব থেকে ভিন্ন।
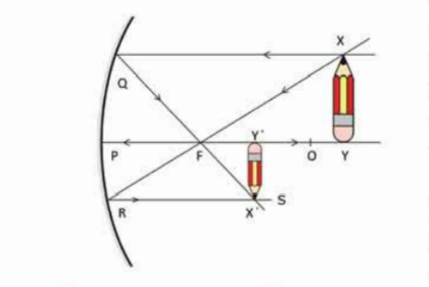
চিত্র 8.24:অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের বাইরে রাখলে প্রতিবিম্বটি
উল্টো এবং ছোট হয়।
8.24 চিত্রে হুবহু একই বিষয় দেখানো হয়েছে।শুধু XY বস্তুটি ফোকাস দূরত্বের দ্বিগুণ থেকে বেশি দুরত্বে রাখা হলে এবারে বস্তুটির প্রতিবিম্বটি হবে ছোট।বস্তুটি যদি ঠিক ফোকাস দূরত্বের দ্বিগুণ দূরত্বে রাখা হতো তাহলে তার প্রতিবিম্বটিও হতো এই একই বিন্দুতেে। শুধু তা-ই নয়, প্রতিবিম্বটির আকার হতো ঠিক বস্তুটির সমান। ফোকাস দূরত্বের বাইরে রাখা এই তিনটি ভিন্ন ভিন্ন ব্যাপার এবারে গুছিয়ে লেখা যেতে পারে। ফোকাস দূরত্বের বাইরে কোনো বস্তুকে রাখা হলে তার প্রতিবিম্ব হবে এ রকম:
(a) প্রতিবিম্বের অবস্থানটা নির্ভর করবে বস্তুটি কোথায় আছে তার ওপর। যতক্ষণ পর্যন্ত বস্তুটি ফোকাস বিন্দু এবং অবতল আয়নার কেন্দ্রের মাঝখানে আছে প্রতিবিম্বের অবস্থানটা হবে কেন্দ্রের বাইরে। বস্তুটি যদি অবতল আয়নার বক্রতার কেন্দ্র থেকে বাইরে থাকে তাহলে তার প্রতিবিম্ব হবে কেন্দ্রের ভেতরে। যদি বস্তুটি ঠিক কেন্দ্রের ওপর থাকে তাহলে প্রতিবিম্বের অবস্থানটাও হবে কেন্দ্রে।
(b) প্রতিবিম্বটি বাস্তব। তাই বস্তুটাকে দিয়ে তার প্রতিবিম্ব যে রকম বের করতে পারি ঠিক সেরকম প্রতিবিম্বটাকে বস্তু ধরা হলে বস্তুটাই হবে তার প্রতিবিম্ব।
(c) প্রতিবিম্বটি উল্টো।
(d) প্রতিবিম্বটির দৈর্ঘ্য নির্ভর করবে এটি কোথায় আছে তার ওপর। যদি এটা ফোকাস বিন্দু এবং বক্রতার কেন্দ্রের মাঝখানে থাকে তাহলে প্রতিবিম্বটির প্রতিবিম্ব হবে বস্তুটি থেকে বড়। যত ফোকাস বিন্দুর কাছাকাছি তত বড়। যদি বস্তুটি বক্রতার কেন্দ্র থেকে বাইরে হয় তাহলে এর আকার হবে আসল বস্তুটি থেকে ছোট। যদি এটা ঠিক বক্রতার কেন্দ্রে থাকে তাহলে প্রতিবিম্বের আকার হবে ঠিক বস্তুটির আকারের সমান।
আমরা জ্যামিতি ব্যবহার করে উত্তল এবং অবতল আয়নার জন্য প্রতিবিম্বের অবস্থান আকার ইত্যাদি বের করেছি। আমরা চাইলে একটিমাত্র সূত্র ব্যবহার করে এই কাজগুলো করতে পারতাম, সূত্রটি হচ্ছে:
এখানে u হচ্ছে আয়নার পৃষ্ঠ থেকে বস্তুর দূরত্ব, v হচ্ছে প্রতিবিম্বের দূরত্ব এবং f হচ্ছে ফোকাস দূরত্ব।
বাস্তব প্রতিবিম্ব খুবই গুরুত্বপূর্ণ একটি ধারণা। আমরা পরের অধ্যায়ে দেখব কেমন করে লেন্স দিয়েও এ রকম বাস্তব প্রতিবিম্ব তৈরি করা যায়। তোমরা দেখতেই পেয়েছ বাস্তব প্রতিবিম্বে সত্যিকারের আলোক রশ্মি থাকে, তাই এটাকে যদি কোনো পর্দায় ফেলা যায়, সেখানে প্রতিবিম্বটি দেখাও সম্ভব হয়। সাধারণ আয়নায় তুমি তোমার চেহারা দেখতে পারবে কিন্তু শুধু সাধারণ আয়না দিয়ে কখনো তোমার চেহারা কোনো পর্দায় ফেলতে পারবে না।
Read more